在上一篇文章中，我们介绍了MoE的一个几何诠释，旨在通过Dense模型的最佳逼近出发来推导和理解MoE。同时在文末我们也说了，给出MoE的计算公式仅仅是开始，训练一个实际有效的MoE模型还有很多细节补，比如本文要讨论的负载均衡（Load Balance）问题。

负载均衡，即"不患寡而患不均"，说白了就是让每个Expert都在干活，并且都在干尽可能一样多的活，避免某些Expert浪费算力。负载均衡既是充分利用训练算力的需求，也是尽可能发挥MoE大参数量潜力的需求。

问题分析

我们知道，MoE的基本形式是 $$ \boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho}} \rho_i \boldsymbol{e}_i $$ 对于传统MoE，$\boldsymbol{\rho}$是一个概率分布（Router），$\boldsymbol{e}_i=\boldsymbol{v}_i$，$\boldsymbol{v}_i$是一个小型FFN（Expert）的输出；而对于我们上一篇推导的几何MoE，$\boldsymbol{\rho}$没有归一化的要求，它预测的是Expert的模长，而$\boldsymbol{e}_i=\boldsymbol{v}_i/\Vert\boldsymbol{v}_i\Vert$预测的是Expert的方向。

不管哪种格式的MoE，实际表现都差不多，只是理解视角的不同。但要注意，虽然MoE的公式给人的感觉是"每遇到一个Token，就去找相应的Expert来计算"，但实际训练时其实是反过来的：先给每个Expert分配好相应的算力，然后将Token分配（Route）到所属的Expert中并行计算，这也就为什么负责打分的$\boldsymbol{\rho}$被称为Router。

这样一来，如果Expert的分配不均衡，就可能出现如下局面：某些Expert（Dead Expert）几乎一直闲置，浪费算力；某些Expert要处理的Token太多，根本忙不过来，只能Token Drop（即放弃处理部分Token）。从理论上来说，出现Dead Expert意味着MoE没有达到预期的参数量，即花了大参数量的显存，结果只训出来小参数量的效果。

所以，不管是从训练还是性能角度看，我们都希望保证Expert的负载均衡。

辅助损失（Auxiliary Loss）

促进负载均衡的常规思路是添加与之相关的损失函数，我们通常称之为"Aux Loss（Auxiliary Loss）"，目前主流用的Aux Loss最早可以追溯到2020年的《GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding》。

介绍Aux Loss之前，我们需要先引入一些新概念。首先，我们已经提到对于一般的MoE来说，$\boldsymbol{\rho}$未必是概率分布，我们将归一化的$\boldsymbol{\rho}$记为$\boldsymbol{p}=[p_1,p_2,\cdots,p_n]$，以及它Top-$k$版为$\boldsymbol{f}=[f_1,f_2,\cdots,f_n]$，其中 $$ p_i = \frac{\rho_i}{\sum_{i=1}^n \rho_i},\qquad f_i = \begin{cases}1/k, & i\in \mathop{\text{argtop}}_k \boldsymbol{\rho} \ 0, & i\not\in \mathop{\text{argtop}}_k \boldsymbol{\rho}\end{cases} $$ 接着我们定义$\boldsymbol{P}=\mathbb{E}[\boldsymbol{p}],\boldsymbol{F}=\mathbb{E}[\boldsymbol{f}]$，这里的$\mathbb{E}$是指对所有样本的所有Token做平均。不难看出，$\boldsymbol{F}$就是Expert当前的负载分布，而$\boldsymbol{P}$则相当于$\boldsymbol{F}$的一个光滑近似。

有了这些记号，我们就可以写出Aux Loss为：
$$ \mathcal{L}_{\text{aux}} = \boldsymbol{F}\cdot \boldsymbol{P} = \sum_{i=1}^n F_i P_i \tag{1} $$

一般文献定义Aux Loss会多乘一个$n$，即它们的Aux Loss等于这里的$n \mathcal{L}_{\text{aux}}$。

此外，有些大型MoE可能会按设备来算Aux Loss，以达到设备内的均衡，减少设备间的通信，这些就各自发挥了。但也有较新的实验显示，强行局部均衡极有可能影响模型最终效果。

直通估计 （Straight-Through Estimator）

不知道大家有没有发现一个奇怪的现象：不管是最早出处、后续文献还是科普文章，总之笔者阅读过的资料中，对Aux Loss的引用都是不加证明的，似乎大家都公认上述Aux Loss能促进均衡是一件显然成立的事情。可真有这么显然易得吗？ 反正笔者是没看出来，所以接下来笔者给出式$(1)$的一种推导思路，由此思路我们还可以自定义其他形式的Aux Loss。

首先，定义均匀分布$\boldsymbol{Q}=(1/n,1/n,\cdots,1/n)$，刚才我们说了$\boldsymbol{F}$就是当前负载分布，因此负载均衡等价于$\boldsymbol{F}=\boldsymbol{Q}$，那么下式就是一个比较直观的Aux Loss：
$$ \mathcal{L}_{\text{aux}} = \frac{1}{2}\Vert\boldsymbol{F} - \boldsymbol{Q}\Vert^2 = \frac{1}{2}\sum_{i=1}^n (F_i - 1/n)^2 \tag{2} $$
问题是$\boldsymbol{F}$是由$\mathop{\text{argtop}}_k$出来的，这意味着上式并不是一个能直接用的可导目标。怎么解决这个问题呢？答案是STE（Straight-Through Estimator）技巧，分别设计前向传播和反向传播的函数。

具体来说，$\boldsymbol{F}$不可导，$\boldsymbol{P}$作为它的光滑近似是可导的，那么我们在反向传播的时候将$\boldsymbol{F}$替换成$\boldsymbol{P}$就行了，即
$$ \mathcal{L}_{\text{aux}} = \frac{1}{2}\Vert \boldsymbol{P} + \text{sg}[\boldsymbol{F}-\boldsymbol{P}] - \boldsymbol{Q}\Vert^2 = \frac{1}{2}\sum_{i=1}^n (P_i + \text{sg}[F_i - P_i] - 1/n)^2 \tag{3} $$
其中$\text{sg}[]$是stop gradient算子，特点是保持前向输出不变，但强制梯度为零。这样改动之后，$\mathcal{L}_{\text{aux}}$ 就是一个切实可行的Aux Loss了，我们可以试求一下它的梯度：
$$ \begin{aligned} \nabla_{\boldsymbol{\theta}}\mathcal{L}_{\text{aux}} &= \frac{1}{2}\nabla_{\boldsymbol{\theta}}\sum_{i=1}^n (P_i + \text{sg}[F_i - P_i] - 1/n)^2 \\ &= \sum_{i=1}^n (P_i + \text{sg}[F_i - P_i] - 1/n) \nabla_{\boldsymbol{\theta}}(P_i + \text{sg}[F_i - P_i] - 1/n)\\ &= \sum_{i=1}^n (F_i - 1/n) \nabla_{\boldsymbol{\theta}}P_i = \nabla_{\boldsymbol{\theta}}\sum_{i=1}^n (F_i - 1/n) P_i\\ &= \nabla_{\boldsymbol{\theta}}\left(\sum_{i=1}^n F_i P_i\right) \end{aligned} $$
这里$\boldsymbol{\theta}$是模型参数。最后的结果表明式$(3)$的梯度等于式$(1)$梯度，这意味着用式$(1)$作为Aux Loss跟式$(3)$在梯度上是等价的，所以就出现了式$(1)$的Aux Loss。

然而，式$(1)$只有等效梯度的意义，但没有Loss的意义，不算一个真正的Loss，比如当$\boldsymbol{F} = \boldsymbol{P}$时我们可以算出式$(1)$等于$1/n$，但实际上我们可以构造出一个不等于$\boldsymbol{P}$的$\boldsymbol{F}$让它小于$1/n$，所以式$(1)$并不是像正常的Loss一样越小越好，最小值也不是$\boldsymbol{F} = \boldsymbol{P}$时取到。

构建Aux Loss的一般形式

上述推导实际上提供了构建Aux Loss的一般思路：首先基于$\boldsymbol{F}$构建符合要求的损失，然后在实现时将$\boldsymbol{F}$替换成$\boldsymbol{P} + \text{sg}[\boldsymbol{F}-\boldsymbol{P}]$。比如，我们知道最大熵也可以将分布推向均衡，因此也可以用熵的相反数来构建Aux Loss：
$$ \mathcal{L}_{\text{aux}} = \sum_{i=1}^n (P_i + \text{sg}[F_i - P_i])\log(P_i + \text{sg}[F_i - P_i]) $$
上式就可以直接用作代码实现，当然如果我们追求简化，也可以类似地求梯度，结果将是
$$ \nabla_{\boldsymbol{\theta}}\mathcal{L}_{\text{aux}} = \nabla_{\boldsymbol{\theta}}\sum_{i=1}^n(P_i + \text{sg}[F_i - P_i]) \log(P_i + \text{sg}[F_i - P_i]) = \nabla_{\boldsymbol{\theta}}\sum_{i=1}^n P_i \log F_i $$
两次简化梯度的过程中，我们都用到了如下恒等式
$$ \sum_{i=1}^n \nabla_{\boldsymbol{\theta}}P_i = \nabla_{\boldsymbol{\theta}}\sum_{i=1}^n P_i = \nabla_{\boldsymbol{\theta}}1 = \boldsymbol{0} $$
这依赖于$\boldsymbol{P}$是一个概率分布，以及目标分布$\boldsymbol{Q}$是均匀分布的事实。而如果我们不追求简化后的等价结果，而是直接用$\boldsymbol{F}\to \boldsymbol{P} + \text{sg}[\boldsymbol{F}-\boldsymbol{P}]$形式的Aux Loss，那么可以不受这两个约束。

比如，$\boldsymbol{P}$作为$\boldsymbol{F}$光滑近似这一点，我们只用到了"$P_i$大$F_i$通常也大"的性质，所以用非归一化的$\mathbb{E}[\boldsymbol{\rho}]$作为$\boldsymbol{P}$通常也没问题，这一点在一些特殊场景（例如有正有负的$\boldsymbol{\rho}$）可能会比较关键，因为此时无法归一化为概率分布。

又比如目标$\Vert\boldsymbol{F} - \boldsymbol{Q}\Vert^2$，显然能将$\boldsymbol{F}$推向任意我们想要的、不一定是均匀的目标分布$\boldsymbol{Q}$。

Loss-Free方案

前面我们主要讨论了通过Aux Loss来促进负载均衡的思路。Aux Loss固然简单直观，但它也有一个明显的缺点——权重不好调——调低了无法促进均衡，调高了容易损害LM Loss，所以业界一直有寻找替代方案的尝试。

接下来要讨论的是名为"Loss-Free"的方案，由DeepSeek在《Auxiliary-Loss-Free Load Balancing Strategy for Mixture-of-Experts》提出。和DeepSeek众多耀眼的开源作品相比，这篇论文也许不算起眼，但在笔者看来，它潜在的学术影响力可能远超其他工作，因为所提方法不仅简单有效，而且极具普适性，堪称经典。

Loss-Free的基本思路

面对负载不均衡，Aux Loss的应对思路是通过额外的损失引导Router给出均衡的打分，而Loss-Free的想法则是换个新的分配思路，即不改变Router现有打分结果，而是改变$\mathop{\text{argtop}}_k \boldsymbol{\rho}$这个分配方式。

其实这个方向此前也有过一些努力。比如2021年Facebook提出了BASE Layer，将Expert的分配视为线性指派问题，即以负载均衡为约束条件，求在该约束之下Router总打分尽可能高的分配结果，这可以用匈牙利算法等来解决。

但该方案需要知道全体Token的打分，所以对于自回归式LLM来说，它只适用于训练，推理还是只能用$\mathop{\text{argtop}}_k \boldsymbol{\rho}$，训练推理存在不一致性，并且由于目前求解算法的限制，它只适用于$k=1$的场景。

相比之下，Loss-Free的做法非常简单且有效，它留意到一个事实，即我们总可以引入一个偏置项$\boldsymbol{b}$，使得$\mathop{\text{argtop}}_k \boldsymbol{\rho} + \boldsymbol{b}$的分配是均衡的，所以它将MoE的形式改为
$$ \boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho}} \rho_i \boldsymbol{e}_i\qquad\to\qquad \boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho} + \boldsymbol{b}} \rho_i \boldsymbol{e}_i $$
这里的$\boldsymbol{b}$是输入无关的向量，由训练过程确定下来，训练完后它就保持不变，因此推理阶段也可以用，换言之训练和推理具有一致的形式。

注意乘以$\boldsymbol{e}_i$的还是$\rho_i$而不是$\rho_i + b_i$，也就是说$\boldsymbol{b}$仅仅参与分配过程而不参与MoE的前向计算，所以我们对$\boldsymbol{b}$或$\boldsymbol{\rho} + \boldsymbol{b}$的正负性都没有特殊要求。

梯度怎么算

怎么训练$\boldsymbol{b}$呢？我们知道，$\boldsymbol{b}$的优化方向自然是促进负载均衡，为此按照上一篇的记号，我们先定义$\boldsymbol{f}=[f_1,f_2,\cdots,f_n]$：
$$ f_i = \begin{cases}1/k, & i\in \mathop{\text{argtop}}_k \boldsymbol{\rho}+\boldsymbol{b} \\ 0, & i\not\in \mathop{\text{argtop}}_k \boldsymbol{\rho}+\boldsymbol{b}\end{cases} $$
以及$\boldsymbol{F}=\mathbb{E}[\boldsymbol{f}]$，这里的$\boldsymbol{F}$自然就是在$\boldsymbol{b}$偏置下Expert当前的负载分布了。借着我们定义均匀分布为$\boldsymbol{Q}=(1/n,1/n,\cdots,1/n)$，那么负载均衡就相当于最小化
$$ \mathcal{L}_{\text{aux}} = \frac{1}{2}\Vert\boldsymbol{F} - \boldsymbol{Q}\Vert^2 = \frac{1}{2}\sum_{i=1}^n (F_i - 1/n)^2 $$
这个目标是不可导的，但有了上一篇的经验，我们知道STE（Straight-Through Estimator）可以解决这个问题。STE的关键是找一个可导且跟$\boldsymbol{F}$具有同增减趋势的量作为$\boldsymbol{F}$的光滑近似，这里我们的优化参数只有$\boldsymbol{b}$，而它正好具有我们期望的性质（增大$b_i$，$i$被选中的概率就更高，那么$F_i$就更大），所以答案就呼之欲出了：
$$ \mathcal{L}_{\text{aux}} = \frac{1}{2}\Vert\boldsymbol{b} + \text{sg}[\boldsymbol{F}-\boldsymbol{b}] - \boldsymbol{Q}\Vert^2 = \frac{1}{2}\sum_{i=1}^n (b_i + \text{sg}[F_i - b_i] - 1/n)^2 $$
它的梯度是
$$ \nabla_{\boldsymbol{b}}\mathcal{L}_{\text{aux}} = \frac{1}{2}\nabla_{\boldsymbol{b}}\Vert\boldsymbol{b} + \text{sg}[\boldsymbol{F}-\boldsymbol{b}] - \boldsymbol{Q}\Vert^2 = \boldsymbol{F} - \boldsymbol{Q} $$
所以用梯度下降（SGD）来更新$\boldsymbol{b}$就是 $$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha (\boldsymbol{F} - \boldsymbol{Q}) $$ 这里$\alpha$是$\boldsymbol{b}$的学习率。不过Loss-Free最终选择的更新规则略有不同，它选择的是符号梯度下降（SignSGD）： $$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha \mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q}) \tag{1} $$ 这个结果其实也很好理解，就是如果$F_i$比$1/n$大，那么就调小一点$b_i$，否则就增大一点$b_i$。 ## 改良版本 除了加$\mathop{\text{sign}}$的符号梯度下降外，笔者发现直接对$\boldsymbol{F} - \boldsymbol{Q}$做RMS Norm（即Normalized SGD），在相同的$\alpha$下往往能达到更好的均衡效果：
$$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha\frac{\boldsymbol{F} - \boldsymbol{Q}}{\text{RMS}(\boldsymbol{F} - \boldsymbol{Q})} $$
这里的$\text{RMS}$是"Root Mean Square"，定义为 $$ \text{RMS}(\boldsymbol{F} - \boldsymbol{Q}) = \sqrt{\frac{1}{n}\sum_{i=1}^n (F_i - Q_i)^2} $$ 不难看出，加$\mathop{\text{sign}}$后的$\mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q})$和加RMS Norm后的$\frac{\boldsymbol{F} - \boldsymbol{Q}}{\text{RMS}(\boldsymbol{F} - \boldsymbol{Q})}$，它们的$\text{RMS}$都是1，因此它们俩尺度上是大致相同的，所以我们可以使用相同的$\alpha$。

简单来说，$\mathop{\text{sign}}$的问题在于不论$F_i$与目标$Q_i$的远近都使用同样的更新幅度，这导致原本就已经跟$Q_i$比较接近的$F_i$反而容易偏离原本已经达到的均衡，从而产生震荡；

而RMS Norm则保留了$F_i-Q_i$之间的相对大小，更新幅度更加自适应一些，理论上更有助于促进均衡，实测效果也多是它更好。

不同视角的合一

原论文在介绍Loss-Free时，并没有上述Aux Loss的推导过程，而是直接给出式$(1)$的更新规则，给人的感觉是给$\boldsymbol{b}$“手搓"了梯度$\mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q})$，这也是它Loss-Free这个名字的来源。

然而，从本文给出的推导可以看出，更新规则$(1)$也完全可以从Aux Loss视角得到，两者是一脉相承的。

看起来Loss-Free最直接的好处是不用调Aux Loss权重了，但它实际上也有个学习率参数$\alpha$要调，尽管原论文已经帮我们搜好$\alpha=0.001$这个默认值，但不可否认这个超参数是存在的。

在笔者看来，Loss-Free的本质创新并不是没有Aux Loss，而是隔离了Aux Loss和LM Loss的优化参数，从而达到了负载均衡和模型能力两不误的效果。

其中最关键一步，是留意到"一个偏置项足以达到负载均衡"这一事实，然后就让Aux Loss只优化新引入的偏置$\boldsymbol{b}$，而LM Loss则优化剩余参数，让Aux Loss对LM Loss的负面作用降到最低。

相比之下，常规的Aux Loss方案需要全体参数来促进负载均衡，而LM Loss优化的也是全体参数，两者的优化方向可能并不完全兼容，因此想找到一个最优的平衡点相对来说就更为困难。

所以，Loss-Free基于"一个偏置项足以达到负载均衡"将两个Loss的优化参数隔离开来，是负载均衡问题的一个绝妙的解决办法。

使用上的细节

尽管Loss-Free已经足够简单明了，但是在使用的时候还要稍微注意一些细节。

首先，对于每个Batch的数据，我们应当先根据LM Loss来更新模型参数，然后再根据式$(1)$来更新$\boldsymbol{b}$。这是因为$\boldsymbol{b}$的更新依赖于全体Token的统计信息$\boldsymbol{F}$，先更新$\boldsymbol{b}$再更新模型其余参数的话，原则上会有泄漏未来信息的风险。虽然直观看来就一个向量$\boldsymbol{b}$泄漏不了多少信息，但这个风险终归是存在的，因此要尽量去规避它。

其次，刚才我们说原论文已经调好$\alpha=0.001$，但这个结果可能跟原论文用Sigmoid作为Router $\boldsymbol{\rho}$激活函数的选择是绑定的。原因也不难想，经过Sigmoid后，每个$\rho_i$相对比较独立，并且都在$(0,1)$内，$\alpha=0.001$相当于说每一步的更新幅度约为千分之一，如果换Softmax、ReLU或者其他激活函数，那么就可能需要重调$\alpha$了。

针对这个问题，笔者建议的做法是解耦Gate和Bias所用的激活函数，即
$$ \boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho} + \boldsymbol{b}} \rho_i \boldsymbol{e}_i\qquad\to\qquad \boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho}^{(\sigma)} + \boldsymbol{b}} \rho_i^{(h)} \boldsymbol{e}_i $$
其中$\boldsymbol{\rho}^{(\sigma)} = \sigma(\boldsymbol{x}\boldsymbol{W}^{(R)}), \boldsymbol{\rho}^{(h)} = h(\boldsymbol{x}\boldsymbol{W}^{(R)})$，$\sigma(\cdot)$是Sigmoid函数，$h(\cdot)$是任意单调且值域非负的函数，说白了就是加上$\boldsymbol{b}$的是Sigmoid激活的打分，这样我们就可以复用$\alpha=0.001$，至于乘上Expert的Gate，我们可以用其他激活函数，只要它的单调性跟Sigmoid一致就行。

此外，由于更新规则$(1)$加了$\text{sign}$函数，因此有可能训出绝对值大于1的$b_i$，整体绝对值还可能越来越大，这些都是正常的，对模型效果不会有影响。

实际上$\boldsymbol{b}$有一个冗余的自由度，因为全体$b_i$都加上同一个常数后，$\mathop{\text{argtop}}_k \boldsymbol{\rho} + \boldsymbol{b}$的结果不变。这个额外的自由度我们可以用来做其他好玩的事情（下文分解）。

延伸思考

除了MoE的负载均衡之外，Loss-Free的思想还可以应用到很多类似问题，比如VQ-VQE的编码表坍缩（Codebook Collapse），就可以用同样思路解决，而且相比之前介绍的”旋转技巧"、"线性变换技巧“显得更自然和普适。

事实上，本文开篇的评价"Loss-Free潜在的学术影响力可能远超其他工作”，正是基于Loss-Free的普适性考虑的。 抛开具体的应用背景，从数学上来看，Loss-Free的贡献可以理解为给出了用梯度下降来求解指派问题的方法。一个经典的线性指派问题可以表示为： $$ \min_f \sum_{i=1}^n c_{i, f(i)} $$ 其中$c_{i,j}$是给定的成本函数，$f$是${1,2,\cdots,n}$到自身的双射。放到本文的背景下，$c_{i,j}$不就相当于$n$个Token、$n$个Expert的打分，所求$f$不就是一个负载均衡的分配方案？

求解此类问题的一般想法是在满足约束条件的空间里搜索尽可能优的解，而Loss-Free则反过来，先构建一个最优但不一定满足约束条件的解：
$$ f(i) = \mathop{\text{argmin}}_j c_{i,j} $$
这个解在分数上肯定是最优的，但不一定满足双射的条件，这里不满足双射就等价于负载不均衡。于是我们引入偏置 $$ f(i) = \mathop{\text{argmin}}_j c_{i,j} + b_j $$ $b_j$初始化为零，然后根据式$(1)$来更新，更新规则说白了就是哪个$j$出现出现次数多，那减少相应的$b_j$，反之增加，直到出现双射为止。

动态调整Expert数量

前面讨论的时候，笔者留了一个悬念：它引入的Bias项有一个冗余的自由度，这个自由度可以用来做另外有趣的事情。这里我们就来讨论这件事。

我们知道，MoE是为每个Token只选择最匹配的$k$个Expert来进行计算，从而在增大参数量的同时还节省了计算量。

然而，当我们仔细思考就会发现，这个策略实际上有明显的可改进之处：直观来看，每个Token的难度并不一样，所以更合理的方案应该是难的Token分配更多的计算资源，简单的token分配更少的资源，这样或许能在同样有限的资源下将效果最大化。

而刚才提到的Bias的额外自由度，恰好可以用来简单地实现这个目标。

设计思想

首先，我们回顾一下，MoE的基本形式是
$$ \boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho}} \rho_i \boldsymbol{e}_i $$
负载不均衡是MoE训练常见的问题，对此研究人员提出了Aux Loss，前面介绍了DeepSeek提出的Loss-Free方案，它将MoE改为
$$ \boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho} + \boldsymbol{b}} \rho_i \boldsymbol{e}_i $$
然后通过调节新引入的Bias项$\boldsymbol{b}$来实现负载均衡。为了实现每个Token可以选择动态数量的Expert，笔者提出的做法是将Loss-Free的形式稍微修改一下：
$$ \boldsymbol{y} = \sum_{i\in \mathop{\text{argwhere}} \boldsymbol{\rho} + \boldsymbol{b} > 0} \rho_i \boldsymbol{e}_i $$
即只要满足$\rho_i + b_i > 0$的Expert就被选中，这样每个Token选出的Expert数量自然是动态的，并且免除了排序的需求，某种程度上看还变得更简化了。

优化目标

$\boldsymbol{b}$的优化目标有两个： 1. 跟Loss-Free一样，要实现负载均匀 2. 要控制每个Token被选中的平均Expert数为$k$（预算控制） 负载均衡依然采样Loss-Free的训练方式。定义记号$\boldsymbol{f} = [f_1, f_2, \cdots, f_n]$ $$ f_i = \begin{cases} 1, & \rho_i + b_i > 0 \ 0, & \rho_i + b_i \leq 0 \end{cases} $$ 然后记$\tilde{\boldsymbol{F}}=\mathbb{E}[\boldsymbol{f}]$，那么$\boldsymbol{F} = \tilde{\boldsymbol{F}}/|\tilde{\boldsymbol{F}}|$就是当前Expert分布，其中$|\tilde{\boldsymbol{F}}|$是$\tilde{\boldsymbol{F}}$的各分量之和。Loss-Free提出的更新公式是：
$$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha \mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q}) $$
其中$\boldsymbol{Q}=(1/n, 1/n, \cdots, 1/n)$是目标的均匀分布。

我们提到多次，$\boldsymbol{b}$存在一个冗余的自由度，体现在对$\boldsymbol{b}$所有分量加上同一个常数，排序结果不变。这样一来，我们可以把更新规则改为
$$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha \left[\mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q}) - \overline{\mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q})}\right] $$
这里向量上面加一横代表该向量的全体分量的均值，是一个标量，向量减标量代表每个分量都减去这个标量。这样一来出来的$\boldsymbol{b}$必然满足$\overline{\boldsymbol{b}}=0$，但不改变负载均衡的效果。

于是我们可以$\overline{\boldsymbol{b}}$这个自由度留给预算控制。 怎么理解呢？很明显，如果给全体$b_i$都加上同一个正数，那么满足$\rho_i + b_i > 0$的几率将会变大，从而总预算也会增大。

所以做法很简单，先算出当前平均预算，不难发现正好是$|\tilde{\boldsymbol{F}}|$，如果它大于$k$，那么就调小一点$\boldsymbol{b}$，反之则增大。整合到上式是
$$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha \left[\mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q}) - \overline{\mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q})} + \mathop{\text{sign}}(|\tilde{\boldsymbol{F}}|- k)\right] $$
如果只想保证预算不超过$k$，而不非要等于$k$，那么可以改为当$|\tilde{\boldsymbol{F}}| < k$时不作改变
$$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha \left[\mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q}) - \overline{\mathop{\text{sign}}(\boldsymbol{F} - \boldsymbol{Q})} + \mathop{\text{sign}}(\max(|\tilde{\boldsymbol{F}}|- k,0))\right] $$

尝试简化

细细品味上面的式子，我们会发现它做了两件事：

  1. 让$\boldsymbol{F}=\tilde{\boldsymbol{F}}/|\tilde{\boldsymbol{F}}|$逼近$\boldsymbol{Q}$
  2. 让$|\tilde{\boldsymbol{F}}|$逼近$k$ 这看起来可以合并成一件事：让$\tilde{\boldsymbol{F}}$逼近$\tilde{\boldsymbol{Q}}=k\boldsymbol{Q}=(k/n,k/n,\cdots,k/n)$。
    于是式前面的公式可以简化为
    $$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha \mathop{\text{sign}}(\tilde{\boldsymbol{F}} - \tilde{\boldsymbol{Q}}) $$
    笔者将两个式子都做了实验，发现它们在效果上大同小异，但是后面的式子的负载均衡和预算控制两个指标在训练前期的抖动都大很多，所以追求稳定性的读者可以优先考虑前两个公式，追求简洁的读者则可以考虑最后一个公式。

考虑到$\mathop{\text{sign}}$只保留了$\tilde{F}_i - \tilde{Q}_i$的符号而忽略了绝对值的大小，笔者也尝试RMS Norm替代$\mathop{\text{sign}}$：
$$ \boldsymbol{b}\leftarrow \boldsymbol{b} - \alpha (\tilde{\boldsymbol{F}} - \tilde{\boldsymbol{Q}})/\Vert\tilde{\boldsymbol{F}} - \tilde{\boldsymbol{Q}}\Vert_{RMS} $$
其中向量的$\Vert\cdot\Vert_{RMS}$是指分量的平方和的平方根。很明显$\mathop{\text{sign}}$的RMS是1，而RMS Norm之后RMS也为1，所以两者更新的数量级相同，可以用同一个$\alpha$。

由于RMS Norm保留了$\tilde{F}_i - \tilde{Q}_i$的相对大小，可以做到误差小的更新也小，所以在波动程度上比$\mathop{\text{sign}}$略小，但也好得不多。 当然，用RMS Norm替换$\mathop{\text{sign}}$来增加稳定性是一个通用技巧，前面推导过程中的式子都可以做这样的替换，这就看个人审美了，总之只是略稳但不多。

初始化方式

解决完$\boldsymbol{b}$的更新规则，我们来考虑$\boldsymbol{b}$的初始化，这是一个有意思但不算十分关键的问题。

按照常规做法，$\boldsymbol{b}$全零初始化且$\boldsymbol{\rho}$用Sigmoid激活，那么初始阶段会把$n$个Expert都选出来，明显超出$\leq k$的预算，这将会导致非常多的Token Drop。

不过，如果我们没有强迫症的话，这并不是很严重的问题，因为模型其他参数通常会加Warmup但$\boldsymbol{b}$通常不加，所以在Warmup的前几步模型就会自动把这个问题解决了。

如果我们介意这一点，那么可以通过调整$\boldsymbol{b}$初始化来控制初始预算。假设Router的输入是$d$维向量，满足零均值、单位方差（有RMSNorm在，近似成立），Router的权重初始化方差为$\sigma^2$，那么Router的Logits近似为零均值、$\sigma^2 d$方差。

有了这些数据，我们可以用正态近似模拟加二分法估算一个初始$\boldsymbol{b}$：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

import numpy as np
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def b_init(n, k, d, sigma, eps=0.1):
    b1, b2 = -1, 0
    std = sigma * d**0.5
    logits = np.random.randn(10000, n) * std
    scores = sigmoid(logits)
    while True:
        b = (b1 + b2) * 0.5
        c = ((scores + b) > 0).sum(1).mean()
        if -eps < c - k < eps:
            return b
        elif c > k:
            b2 = b
        else:
            b1 = b

b_init(32, 4, 1024, 6e-3)

代码中考虑的是Sigmoid激活，所以搜索区间是$[-1, 0]$，如果是其他激活函数请自行调整。不过这里的建议跟前面聊到的思路是相同的，即加b的ρ可以统一用Sigmoid激活，乘上Expert的ρ才考虑用别的激活函数。

相关工作

其实，已经有一些工作尝试过动态选择Expert数目的MoE设计，下面简单列举一些笔者搜到的工作，并从个人的审美角度做一些简单的评析。

比较朴素的做法是AdaMoE和MoE++，它们在Expert中混入了一些低计算成本的Expert，如空白Expert、复制Expert、常数Expert，同时也鼓励负载均衡，这样当Token选中这些简单Expert时，等价于少选择了其他标准的Expert，从而间接地实现了动态数目。这样做的好处是可以复用原本Top-k MoE的基建，但同时也欠缺了一些灵活性。

另外一个朴素的想法是将Top-k选择改为Top-p，出自《Harder Tasks Need More Experts: Dynamic Routing in MoE Models》。这个转换看上去很自然，但实际上有颇多问题，比如无法准确控制平均预算，因为当ρ接近均匀分布时Top-p的比例会非常大，所以原论文又新增了一项熵损失来让ρ远离均匀分布。总的来说，个人感觉它引入的问题比收益更明显。

一个比较独特的做法是Ada-K Routing，它新增一个模块来预测要激活的Expert数，然后用强化学习来训练，这样做在原理上没问题，但引入强化学习无疑会增加训练复杂性。DA-MoE则利用Attention分数来识别重要Token，为其分配更多Expert，但感觉不够本质，因为“MoE”原则上不局限于FFN层，一旦用到Attention上，不就没有Attention分数可用了？

形式上跟本文做法最相似的可能是ReMoE，它同样是基于零阈值来选择Expert，但选择了Aux Loss的方式来实现负载均匀以及预算控制，同时又混合了手搓梯度的思想来控制Aux Loss权重，总体来看多了点糅合感。

本文则延续了Loss-Free的思想，利用b的额外自由度来调控这个阈值，从而以最小的改动实现了动态Expert数目。

均匀分布的反思: Shared Expert和Fine-Grained Expert

如果说Meta的LLAMA系列为Dense模型确立了标准架构，那么DeepSeek或许就是MoE标准架构的奠基者。

当然，这并非指DeepSeek首创了MoE，也不是说它的MoE不可超越，而是指DeepSeek对MoE所提的一些改进，很可能都是效果增益比较显著的方向，从而逐渐成为MoE的标配。

这其中，包括我们在前面章节介绍的Loss-Free负载均衡方案，还有将要介绍的Shared Expert、Fine-Grained Expert策略。

说到负载均衡，它无疑是MoE一个极为重要的目标，前面的几个章节，可以说都在围绕着它展开。然而，已有读者逐渐意识到，这里边有个尚未回答的本质问题：抛开效率上的需求不谈，均匀分布就一定是效果最好的方向吗？

这里就带着这个疑问，去理解Shared Expert、Fine-Grained Expert。

共享专家

让我们再次回顾MoE的基本形式
$$ \boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho}} \rho_i \boldsymbol{e}_i $$
除此之外，前文中的Loss-Free将$\mathop{\text{argtop}}_k \boldsymbol{\rho}$替换换成$\mathop{\text{argtop}}_k \boldsymbol{\rho}+\boldsymbol{b}$，还有在前文我们将它推广成$\mathop{\text{argwhere}} \boldsymbol{\rho}+\boldsymbol{b} > 0$，但这些变体跟Shared Expert技巧都是正交的，因此接下来只以最基本的形式为例。

Shared Expert将上式改为
$$ \boldsymbol{y} = \sum_{i=1}^s \boldsymbol{e}_i + \sum_{i\in \mathop{\text{argtop}}_{k-s} \boldsymbol{\rho}_{[s:]}} \rho_{i+s} \boldsymbol{e}_{i+s} $$
也就是说，将原本的$n$选$k$，改为$n-s$选$k-s$，另外$s$个Expert则必然会被选中，这部分就被称为"Shared Expert"，刚出来那会我们还戏称为"常任理事国"，剩下的$n-s$个Expert则被称为"Routed Expert"。

其中，Shared Expert的数目$s$不会太大，通常是1或2，太大反而会让模型"冷落"了剩下的Routed Expert。

需要指出的是，开启Shared Expert前后，总Expert数都是$n$，激活的Expert都是$k$，所以Shared Expert原则上不增加模型参数量和推理成本。但即便如此，DeepSeekMoE和我们自己的一些实验显示，Shared Expert依然能一定程度上提升模型效果。

多种理解

我们可以从多个视角理解Shared Expert：

  1. 残差视角：指出Shared Expert技巧实际上是将原本学习每一个Expert，改为学习它跟Shared Expert的残差，这样能降低学习难度，还会有更好的梯度。

  2. 教学类比：DeepSeek的说法是将共同知识压缩到这些Shared Expert中，减轻Routed Expert之间的冗余。如果将Routed Expert类比成中学各个学科的老师，那么Shared Expert就是类似"班主任"的存在。

  3. 几何角度：Expert之间的不可避免的共性，几何意义是它们的向量夹角小于90度。我们可以将Shared Expert理解成这些Routed Expert的均值，通过学习减去均值后的残差，使得正交假设更容易成立。

比例因子

我们将前面带上Shared Expert的式子一般地写成
$$ \boldsymbol{y} = \sum_{i=1}^s \boldsymbol{e}_i + \lambda\sum_{i\in \mathop{\text{argtop}}_{k-s} \boldsymbol{\rho}_{[s:]}} \rho_{i+s} \boldsymbol{e}_{i+s} $$
由于Routed Expert带有权重$\rho_{i+s}$而Shared Expert没有，以及Routed Expert的数目通常远大于Shared Expert数目（即$n - s \gg s$）等原因，它们的比例可能会失衡，因此设置合理的$\lambda$尤为重要。

在论文《Muon is Scalable for LLM Training》中提出，适当的$\lambda$应使得两者在初始化阶段模长接近一致。

具体计算方法：

  1. 假设每个Expert在初始化阶段具有相同的模长（设为1）且两两正交
  2. 假设Router的logits服从标准正态分布
  3. 通过数值模拟计算$\lambda$：
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np 

def sigmoid(x): 
	return 1 / (1 + np.exp(-x)) 
	
def softmax(x): 
	return (p := np.exp(x)) / p.sum() 
	
def scaling_factor(n, k, s, act='softmax', renorm=False): 
	factors = [] 
	for _ in range(10000): 
		logits = np.random.randn(n - s) 
		p = np.sort(eval(act)(logits))[::-1][:k - s] 
		if renorm:
			p /= p.sum() 
		factors.append(s**0.5 / (p**2).sum()**0.5) 
	return np.mean(factors) 
	
# DeepSeek-V2配置
scaling_factor(162, 8, 2, 'softmax', False) # ≈16 
# DeepSeek-V3配置 
scaling_factor(257, 9, 1, 'sigmoid', True) # ≈2.83

非常巧的是，这个脚本的模拟结果跟DeepSeek-V2、DeepSeek-V3的设置都很吻合。

其中，DeepSeek-V2有n=162,k=8,s=2，Softmax激活并且没有重归一化，上述脚本的模拟结果约等于16，而DeepSeek-V2的λ正好是16来源；DeepSeek-V3则有n=257,k=9,s=1，Sigmoid激活且重归一化，脚本的结果大约是2.83，而DeepSeek-V3的λ则是2.5来源。

非均匀性

回到文章开头的问题：均衡一定是效果最好的方向吗？看起来Shared Expert给了一个参考答案：未必。因为Shared Expert也可以理解为某些Expert一定会被激活，于是整体来看，这将导致一个非均匀的Expert分布：
$$ \boldsymbol{F} = \frac{1}{s+1}\bigg[\underbrace{1,\cdots,1}_{s\text{个}},\underbrace{\frac{1}{n-s},\cdots,\frac{1}{n-s}}_{n-s\text{个}}\bigg] $$
实际上，非均匀分布在现实世界随处可见，所以均匀分布并非最优方向其实应该很容易接受。还是以前面的中学老师类比为例，同一个学校各个学科的老师数量其实是不均匀的，通常是语文、数学、英语最多，物理、化学、生物次之，体育、美术更少（还经常生病）。更多非均匀分布的例子，大家可以搜索一下Zipf定律。

总而言之，现实世界的非均匀性，必然会导致自然语言的非均匀性，从而导致均匀分布的非最优性。当然，从训练模型的角度看，均匀分布还是更容易并行和扩展，所以单独分离出一部分Shared Expert，剩下的Routed Expert仍然希望它均匀，是实现非均匀性的一种对双方都友好的折中选择，而不是直接让Routed Expert对齐一个非均匀分布。

刚才说的是训练，那推理呢？推理阶段可以事先预估Routed Expert的实际分布，并且不需要考虑反向传播，所以只要细致地进行优化，理论上可以做到效率不降的。但由于现在MoE的推理基建都是针对均匀分布设计的，并且单卡显存有限等实际限制，所以我们仍旧希望Routed Expert能均匀来实现更好的推理效率。

细颗粒度

除了Shared Expert外，DeepSeekMoE所提的另一个改进点是Fine-Grained Expert，它指出在总参数量和激活参数量都不变的情况下，Expert的颗粒度越细，效果往往越好。

比如，原本是n选k的Routed Expert，现在我们将每个Expert缩小一半，然后改成2n选2k，那么总参数量和激活的参数量都还是一样的，但后者表现往往更好。原论文的说法是这样丰富了Expert组合的多样性。

当然，我们也可以有其他理解，比如说将Expert进一步分割成更小的单元，那么每个Expert可以专注于更狭窄的知识领域，从而实现更精细的知识分解，等等。但要注意，Fine-Grained Expert并非是无成本的，n越大，Expert之间的负载往往越不均衡，并且Expert之间的通信和协调成本也会增加，所以n也不能无限增加，有一个效果和效率都友好的舒适区间。

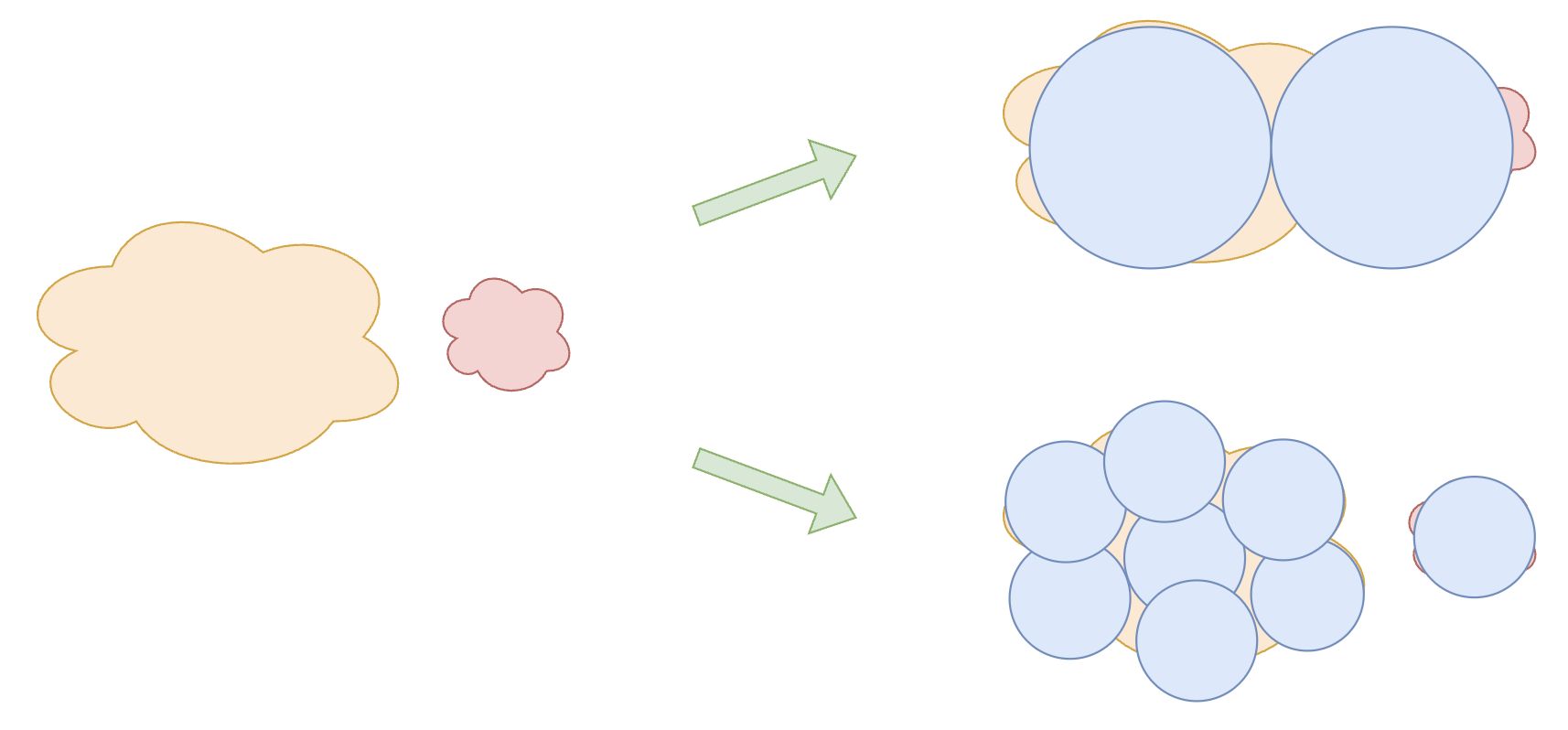
关于Fine-Grained Expert的有效性，笔者这里提出另外一种不大容易察觉的解释，它跟本文的主题有关：更多数量、更细颗粒度的Expert，可以更好地模拟现实世界的非均匀性。

以下图为例，假设知识可以分为一大一小两类，每个Expert则是一个圆，如果我们用2个大圆去覆盖，那么存在一定的遗漏和浪费，而如果改用8个总面积相同的小圆，那么就可以覆盖得更为细致，因此效果更优。

细颗粒度理解